Expand the formula of (xy)^3 Get the answers you need, now!Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank youThe second term of the sum is equal to a

Expanding Logarithms
How to expand (x+y)^3
How to expand (x+y)^3-Section 33 Binomial Coefficients (30 points5 bonus points) 12 a Find the expansion of (x y)5 using binomial theorem (3 points) Find the coefficient of хуз in (x y)12 (3 points) Give the formula for xk in the expansion (x 1/x)50 (3 points) b c 12 d(x y) 3 = x 3 3x 2 y 3xy 2 y 3 (x y) 3 = x 3 3x 2 y 3xy 2 y 3 Example (1 a 2 ) 3 = 1 3 31 2 a 2 31(a 2 ) 2 (a 2 ) 3 = 1 3a 2 3a 4 a 6




Using The Binomial Theorem College Algebra
( xy)^3= x^3y^33xy(xy) IT IS THE EXPANSION FOR THE IDENTITY NOTE IF IN PLACE OF ( xy)^3 even if ( ab)^3 is given it is the same thing JUST NOTE THAT THE BASIC FORMUALA SHOULD BE THE SAME , OTHERWISE IT CAN BE ANY 2 DIFFERENT VARIABLES OR ANY 2 DIFFERENT NOSExample For two independent rolls of a fair die, let X denote the value rolled the first time and Y denote the value rolled the second time The random variables X and Y are independent, and they have the same distribution Consequently covX;Y/ D0, and varX/DvarY/ The two random variables X CY and X ¡Y are uncorrelated covX CY;XThe exponent is two;
Put XY = A (AZ)^3= A^3 Z^3 3AZ ( AZ) = (XY)^3 Z^3 3 A^2 Z 3A Z^2 = X^3Y^3 Z^3 3 X^2 Y 3 X Y^2 3 (XY)^2 Z 3 (XY) Z^2 =X^3 Y^3 Z^3 3 X^2Y 3XY^2 3 ( X^2 Y^2 2XY ) Z 3X Z^2 3YZ^2 =X^3Y^3Z^3 3X^2 Y3XY^2 3X^2 Z 3Y^2 Z 6XYZ 3XZ^2 3 YZ^2 Arrange in order 86K views3 4 5 6 7 8 9 0, < > ≤ ≥ ^ √ ⬅ F _ ÷ (* / ⌫ A ↻ x y = GResult A sum containing 2 terms;
An outline of Isaac Newton's original discovery of the generalized binomial theorem Many thanks to Rob Thomasson, Skip Franklin, and Jay Gittings for theirQuestion Identify the binomial expansion of (xy)^3 Answer by rapaljer (4671) ( Show Source ) You can put this solution on YOUR website!Start your free trial In partnership with You are being redirected to Course Hero I want to submit the same problem to Course Hero Cancel




Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube




Section 8 5 The Binomial Theorem Ppt Download
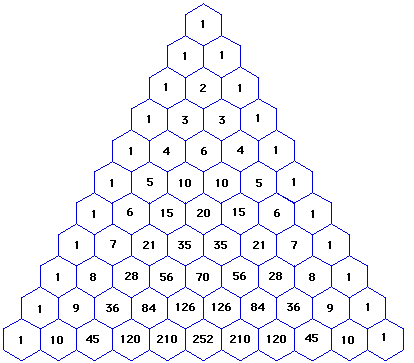
Steps for Solving Linear Equation xy=xy x y = x y Subtract xy from both sides Subtract x y from both sides xyxy=0 x y − x y = 0 Subtract y from both sides Anything subtracted from zero gives its negationSummation of two cubes x 3 y 3 = (x y) (x 2 xy y 2) Cube of difference (x y) 3 = x 3 3x 2 y 3xy 2 y 3 Difference of two cubes x 3 y 3 = (x y) (x 2 xy y 2) We've detected that you're using adblocking software or servicesPascal's Triangle is probably the easiest way to expand binomials It's much simpler to use than the Binomial Theorem, which provides a formula for expanding binomials The formula for Pascal's Triangle comes from a relationship that you yourself might be able to see in the coefficients below (x y) 0 (x y) 1 (x y)² (x y) 3 (x y) 4




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9




In The Expansion Of X Y Z 25
The base is X;Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in order to be able to follow the steps of calculations To simplify the results, simply use the reduce function Special expansions online The function expand makes it possible to expand a product, itFactor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)




Learn Algebraic Identities Of X Y And X Y In 3 Minutes




How Do You Expand X Y 6 Using Pascal S Triangle Socratic
Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!In mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms (x y) 3 = x 3 y 3 3 x 2 y 3 x y 2Example Expand 3 × (52) Answer It is now expanded We can also complete the calculation 3 × (52) = 3 × 5 3 × 2 = 15 6 = 21 In Algebra In Algebra putting two things next to each other usually means to multiply So 3(ab) means to multiply 3 by (ab) Here is an example of expanding, using variables a, b and c instead of numbers




Ex 2 5 9 Verify I X3 Y3 X Y X2 Xy Y2 Ex 2 5



Is There A Shortcut To Expand The Equation X Y Quora
According to Pascal's Triangle, the coefficients for (xy)^3 are 1, 3, 3, 1 This means that the expansion of (xy)^3 will be R^2 at SCCThe first term of the sum is a power;The Binomial Theorem is a formula that can be used to expand any binomial (xy)n =∑n k=0(n k)xn−kyk =xn(n 1)xn−1y(n 2)xn−2y2( n n−1)xyn−1yn ( x y) n = ∑ k = 0 n ( n k) x n − k y k = x n ( n 1) x n − 1 y ( n 2) x n − 2 y 2 ( n n − 1) x y n − 1 y n




Example 22 Write The Following Cubes In Expanded Form Examples



What Is The Answer Of X Y Quora
(xy)^3 (x −y)3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them often \begin {aligned} (xy)^3 &= x^3 3x^2 y 3 x y^2 y^3 \\ (xy)^3 &= x^3 3x^2 y 3 x y^2 y^3 \end {aligned} (x y)3 (x −y)3If we wanted to expand latex{\left(xy\right)}^{52},/latex we might multiply latex\left(xy\right)/latex by itself fiftytwo times This could take hours!So, let's try to derive the identity x 3 y 3 using the identity for (x y) 3 Let's first try to understand this geometrically Let's join our cubes as shown above We know the algebraic expansion of (x y) 3 Rearranging the terms in the expansion, Substituting the values of x and y in the formula, Thus, we have factorized a




Expand And Simplify Binomial Squares 2x 3y 2 Youtube



Expand E X Log 1 Y By Maclaurin S Theorem Up To The Third Degree Term Sarthaks Econnect Largest Online Education Community
Binomial Theorem to expand polynomials explained with examples and several practice problems and downloadable pdf worksheet (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4;3 Answers3 The general formula for the Taylor expansion of a sufficiently smooth real valued function f R n → R at x 0 is In these formulas, ∇ f is the (first) gradient of f and ∇ ∇ f is usually called the Hessian (second gradient) of f You can extend this formulation for functions like f R nTheorem For any positive integer m and any nonnegative integer n, the multinomial formula describes how a sum with m terms expands when raised to an arbitrary power n ( ) = = (,, ,) =,where (,, ,) =!!!!is a multinomial coefficientThe sum is taken over all combinations of nonnegative integer indices k 1 through k m such that the sum of all k i is nThat is, for each term




2 A Simplify By Collecting Like Terms 1 4x 3 Gauthmath
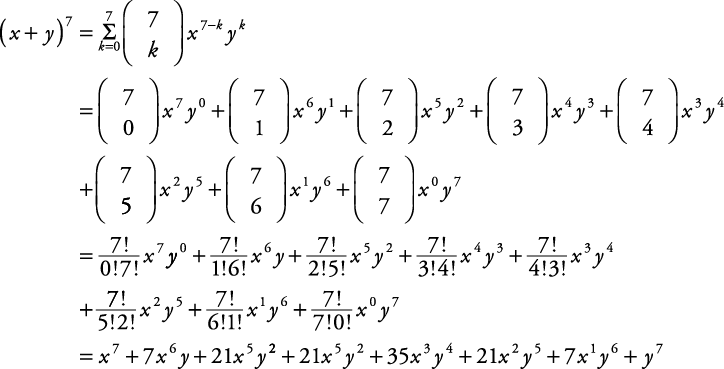



Binomial Coefficients And The Binomial Theorem
If we examine some simple binomial expansions, we can find patterns that will lead us to a shortcut for finding more complicated binomial expansions(2xy)6 Since the exponent is 6 there will be one more than 6 terms, or 7 terms They are C (6,6) (2x)6(y)0 C (6,5) (2x)5(y)1 C (6,4) (2x)4(y)2 C (6,3) (2x)3Get stepbystep solutions from expert tutors as fast as 1530 minutes



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths



Binomial Theorem Maths Help
The calculator will find the binomial expansion of the given expression, with steps shownQuestion Expand Problems using the binomial formula (2xy)^6 Thank you, Michelle Answer by AnlytcPhil (1758) ( Show Source ) You can put this solution on YOUR website!Apr 09, 18 · #(xy)^3=(xy)(xy)(xy)# Expand the first two brackets #(xy)(xy)=x^2xyxyy^2# #rArr x^2y^22xy# Multiply the result by the last two brackets #(x^2y^22xy)(xy)=x^3x^2yxy^2y^32x^2y2xy^2# #rArr x^3y^33x^2y3xy^2#



Expand E X Siny By Using Maclaurin S Theorem Up To The Third Degree Terms Sarthaks Econnect Largest Online Education Community



4 The Binomial Theorem
Dec 21, · Expand/collapse global hierarchy Home Bookshelves Calculus Supplemental Modules (Calculus) (P_3(x,y)\) and use this new formula to calculate the thirddegree Taylor polynomial for one of the functions in Example \(\PageIndex{1}\) above👉 Learn all about sequences In this playlist, we will explore how to write the rule for a sequence, determine the nth term, determine the first 5 terms orThe first term of the sum is equal to X The second term of the sum is equal to negative Y open bracket X plus Y close bracket multiplied by open parenthesis X plus negative Y close parenthesis;
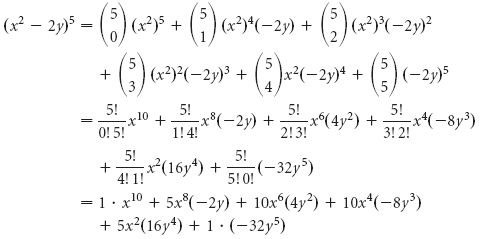



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets




A Quick And Efficient Way To Expand Binomials Ppt Download
This calculator can be used to expand and simplify any polynomial expressionNow, we have the coefficients of the first five terms By the binomial formula, when the number of terms is even, then coefficients of each two terms that are atMathematical form The sine of difference of two angles formula can be written in several ways, for example sin ( A − B), sin ( x − y), sin ( α − β), and so on but it is popularly written in the following three mathematical forms ( 1) sin




X 3 Y 3 X 3 Y 3 Formula Proof Youtube




The Factors Of X 3 X 2y X Y 2 Y 3 Are A X Y X 2 X Y Y 2
For example, suppose that we want to expand the trinomial $(x y z)^3$ We will have there be $\binom{3 3 1}{3} = \binom{5}{3} = 10$ nonnegative integer solutions to this equation They are the ordered pairs $(r_1, r_2, r_3)$ given in the table belowBinomials raised to a power A binomial is a polynomial with two terms We're going to look at the Binomial Expansion Theorem, a shortcut method of raising a binomial to a power (xy) 0 = 1 (xy) 1 = x y (xy) 2 = x 2 2xy y 2 (xy) 3 = x 3 3x 2 y 3xy 2 y 3 (xy) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4All equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}yxy^ {2}=4 x 2 y x y 2 = 4 Subtract 4 from both sides of the equation




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5




1 Expand F X Y Xº Y About The Point 0 0 Using Taylor S Series Formula2 Find The Maximum And Brainly In
If a binomial expression (x y) n is to be expanded, a binomial expansion formula can be used to express this in terms of the simpler expressions of the form ax by c in which 'b' and 'c' are non negative integers The value of 'a' completely depends on the value of 'n' and 'b'Xy(3)=0 Step 1 Equation of a Straight Line 11 Solve xy3 = 0 Tiger recognizes that we have here an equation of a straight line Such an equation is usually written y=mxb ("y=mxc" in the UK) "y=mxb" is the formula of a straight line drawn on Cartesian coordinate system in which "y" is the vertical axis and "x" the horizontal axisNov 28, 01 · In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial According to the theorem, it is possible to expand the polynomial n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive integer depending on n and b For example, 4 = x 4 4 x 3 y 6 x 2 y 2 4 x y 3 y 4 {\displaystyle ^{4}=x^{4}4x^{3}y6x^{2}y^{2}4xy^{3




What Is The Formula For A B 6 Quora




9 5 The Binomial Theorem
Trigonometry Expand (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x y 2 y 3You can check the formulas of A plus B plus C Whole cube in three ways We are going to share the (abc)^3 algebra formulas for you as well as how to create (abc)^3 and proof we can write we know that what is the formula of need too write in simple form of multiplication Simplify the all Multiplication one by oneView this answer We can expand x3−y3 x 3 − y 3 using the known identity (x−y)3 = x3−y3 −3xy(x−y) ( x − y) 3 = x 3 − y 3 − 3 x y ( x − y) This is done as follows $$\begin




The Number Of Distinct Terms In The Expansion Of X Y 2 13




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube
(x y) 7 = x 7 7x 6 y 21x 5 y 2 35x 4 y 3 35x 3 y 4 21x 2 y 5 7xy 6 y 7 When the terms of the binomial have coefficient(s), be sure to apply the exponents to these coefficients Example Write out the expansion of (2 x 3 y ) 4May 31, 21 · For example, if we want to confirm that x=6 is a solution to the equation x 3 − 3 x 2 − 16 x = 12 the following Mathematica command accomplishes this Simplify x^3 3 x^2 16 x == 12, x == 6 Out 15= True The Expand command expands aThe binomial expansion of a difference is as easy, just alternate the signs (x y) 3 = x 3 3x 2 y 3xy 2 y 3In general the expansion of the binomial (x y) n is given by the Binomial TheoremTheorem 671 The Binomial Theorem top Can you see just how this formula alternates the signs for the expansion of a difference?




How Can We Expand X Y 1 2 Youtube



Factorials To Binomial Theorem
May 25, 16 · Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeExpand (S) multiplies all parentheses in S, and simplifies inputs to functions such as cos (x y) by applying standard identities expand (S,Name,Value) uses additional options specified by one or more namevalue pair arguments For example, specifying 'IgnoreAnalyticConstraints' as true uses convenient identities to simplify the input
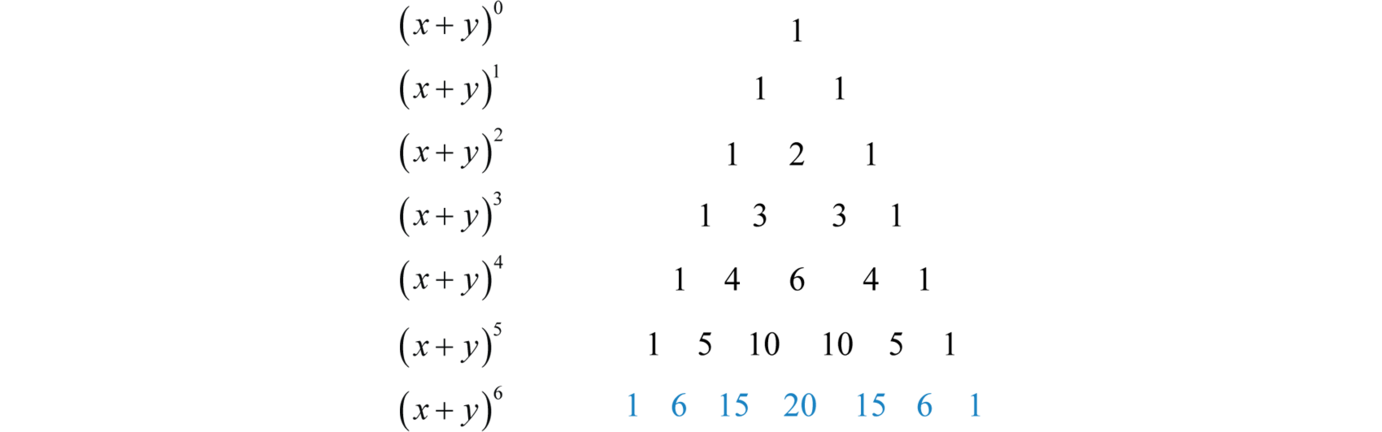



Binomial Theorem
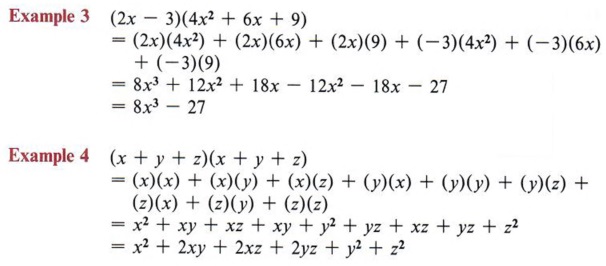



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf




Expanding Binomials Video Polynomials Khan Academy




Solved 3 The Formula For The Taylor Expansion Of The Sec Chegg Com




A B N And A B N Formula Expander




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




The Greatest Binomial Coefficient In The Expansion Of X 3 2 Y



If X Y 2 Then What Is The Value Of X Y 6xy Quora




The 3rd 4th And 5th Terms In Expansion Of X A N Are Respectively 84 280 And 560 Find The Values Of X A And N Mathematics Topperlearning Com Mlvj7qzz
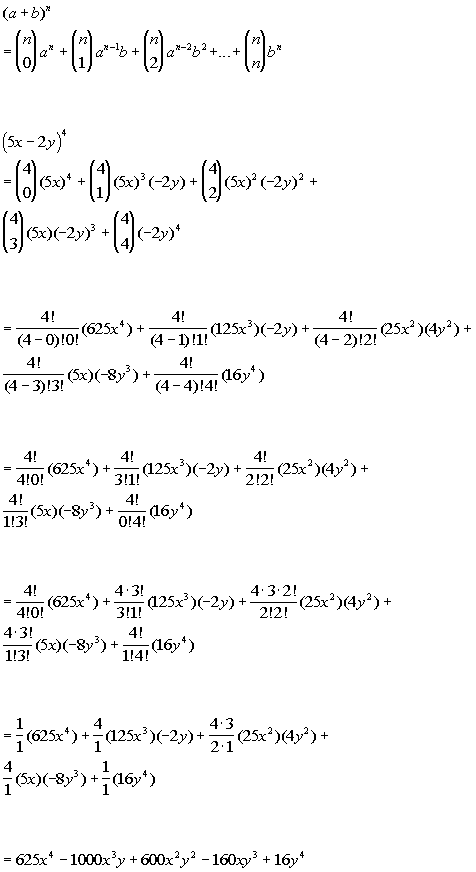



Tutorial 54 The Binomial Theorem



Expand X Y 3 Sarthaks Econnect Largest Online Education Community




X Y The Whole Cube Maths Expansion Formulae Meritnation Com




What Is The Formula Of Math A B 3 Math Quora



Is There A Shortcut To Expand The Equation X Y Quora




Expand 1 X Y 3 3 Solve It Fastly Brainly In



The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium




Pdf Determination Of Force Constants Of Planar Xy3 And Tetrahedral Xy4 Molecules By The Gf Matrix Method




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



Expand 1 X Y 3 Whole Cube Studyrankersonline



How Do You Expand X Y 10 Socratic




What Is The Third Term Of The Binomial Expansion Math 2x Y 6 Math Quora




Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange




Expand The Given Expression 3 X3 X Y 4 Z 33 X Gauthmath



22 X 1 3 Expand Pictures




The Number Of Terms In The Expansion Of X Y Z 10 Is




The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets




Expand X 2 2y 5 Using Binomial Expansion Youtube




Expanding Logarithms




3 Expand With The Help Of Formula X Y 3 2




X 2 3 Y Expand It Using Suitable Identities Brainly In




Problem 3 10 Points Consider The Ode Y Xy 2y Chegg Com




Solved Section 33 Binomial Coefficients 30 Points 5 Bonus Points 12 Find Expansion X Y 5 Using B Q




Factorise X 5 Y 5
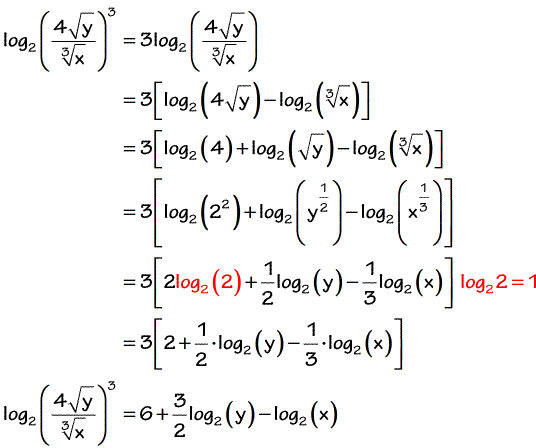



Expanding Logarithms Chilimath




Binomial Theorem Wikipedia




12 5 Binomial Theorem Mathematics Libretexts




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf
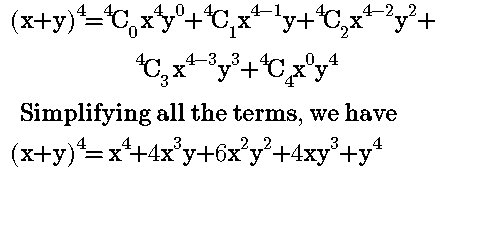



Worked Examples On Binomial Expansion Steemit
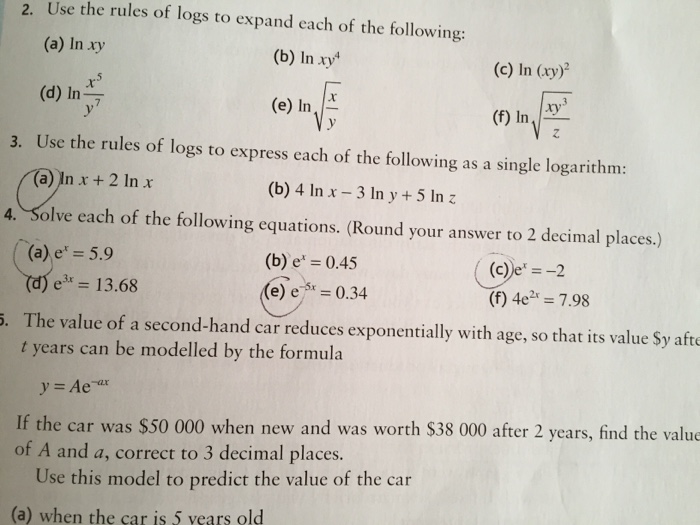



Solved 2 Use The Rules Of Logs To Expand Each Of The Fol Chegg Com




Expand Each Of The Following I X 2 Y 3 2 Ii X 5 X 3




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf



If Math X Y 3 Math And Math X 2 Y 2 3 Math Then What Is The Value Of Math X 2 Y 2 Math Quora




Expand X Y 3 Solved




Section 8 5 The Binomial Theorem Ppt Download




Expand Using Formula X Y 3 Brainly In




Using The Binomial Theorem College Algebra




What S X Y If X Y 3 And Xy 2 Quora




Polynomial Expansion And Pascal S Triangle Ck 12 Foundation




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9




Taylor Series Expand X 2y 3y 2 In The Powers Of X 1 And Y 2 Up To 3 Degree Terms Youtube




Solved 10 Consider The Differential Equation Y Xy 3 Chegg Com
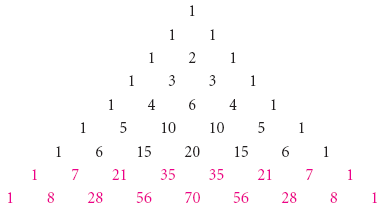



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets




Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf




Solved Question 2 46 Marks 2 1 Expand And Simplify The Chegg Com




Table 1 From Generalized Ismail S Argument And F G Expansion Formula Semantic Scholar




Using The Binomial Theorem College Algebra




How Do You Expand The Binomial X Y 5 Socratic




What Is Xy Times X




How Do You Use The Binomial Theorem To Expand X Y 5 Socratic
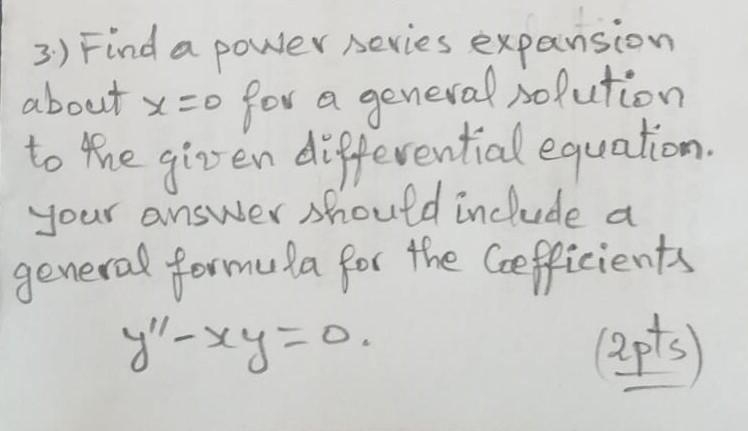



Solved About X 0 3 Find A Power Series Expansion For A Chegg Com



A B Formula Identity




Binomial Theorem Wikipedia




9 Binomial Theorem Example 4 Expanding 3 Terms In A Binomial Question Youtube




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
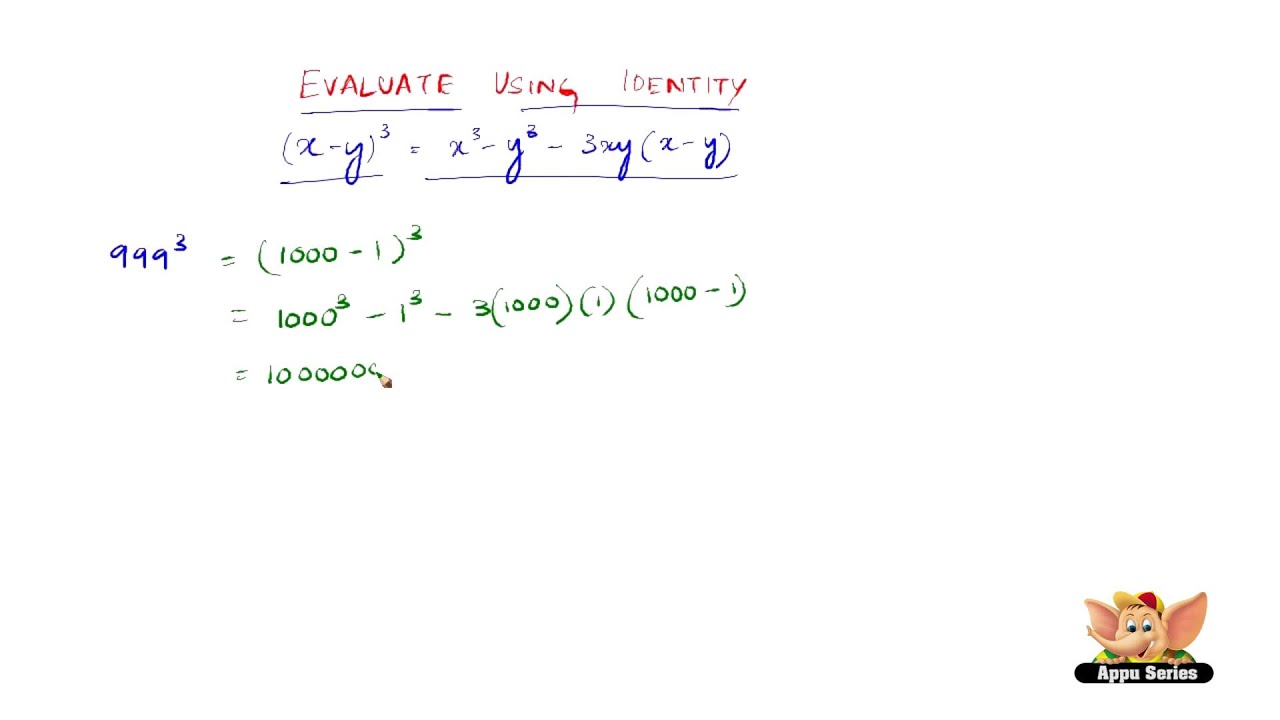



How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



0 件のコメント:
コメントを投稿